R07 1級電気工事施工管理技術検定 第一次検定問題 No.03

問題

　図に示す回路において、検流計の指示値が０となるとき、抵抗\( R \)[Ω]とインダクタンス\( L \)[mH]の値と組合せとして、適当なものはどれか。
　ただし、相互インダクタンスは無視するものとする。

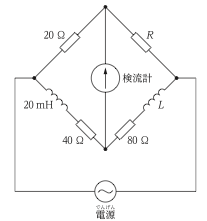
ホイートストンブリッジ回路で検流計が0になる条件は、対角線上のインピーダンスの積が同一の場合となるため、

\( R_1 R_3 = R_2 R_4 \)

\( \displaystyle R_1=20,　R_2=R,　R_3=80+j \omega L,　R_4=j \omega ( 20*10^{-3} )+40 \)

\( \displaystyle 20*(80+j \omega L)=R*(j \omega ( 20*10^{-3} )+40) \)

\( \displaystyle 1600+20*j \omega L =R*j \omega ( 20*10^{-3}) +R*40 \)

実数と虚数のそれぞれの項は等しいため、

\( \displaystyle 1600 = R*40 \)

\( \displaystyle R = 40 \) [Ω]

\( \displaystyle 20*j \omega L =R*j \omega ( 20*10^{-3}) \)

\( \displaystyle 20* L =40* ( 20*10^{-3}) \)

\( \displaystyle L =2* ( 20*10^{-3}) =40*10^{-3} = 40 \)[mH]