R07 1級電気工事施工管理技術検定 第一次検定問題 No.01

図に示す回路において，電圧\(V＝10V\)を加えたとき，静電容量\(C_1 = 2\mu \mathrm{F} \) ，\(C_2= 4\mu \mathrm{F} \) のコンデンサに蓄えられる合計のエネルギー\(W\)の値 \( \mathrm{[J]} \) として，正しいものはどれか。

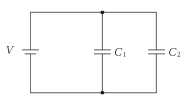
コンデンサの合成静電容量 \(C\)
コンデンサの並列接続時の合成静電容量 \(C\) は、以下の式で示される。
\( C = C_1+C_2 \)

よって、この回路のコンデンサの合成静電容量 \(C\) は、
\( \begin{align}
C &= C_1+C_2 \\
&= 2\mu \mathrm{F} + 4\mu \mathrm{F} \\
&= 6\mu \mathrm{F}
\end{align} \)

コンデンサの静電エネルギー \(W\)
コンデンサの静電エネルギー \(W \mathrm{[J]} \) は、コンデンサの静電容量 \(C \mathrm{[F]} \) 及びコンデンサに加わる電圧 \(V \mathrm{[V]} \) とすると、
\( \displaystyle W = \frac{1}{2} CV^2 \)

よって、この回路のコンデンサに蓄えられる合計のエネルギー \(W \mathrm{[J]} \) は、
\( \begin{align} \displaystyle
W &= \frac{1}{2} CV^2 \\
&= \frac{1}{2} \times 6\mu \mathrm{F} \times 10^2 \mathrm{[V]} \\
&= \frac{1}{2} \times 6 \times 10^{-6} \times 10^2 \\
&= 3 \times 10^{-4} \mathrm{J} \\
\end{align} \)