R07 1級電気工事施工管理技術検定 第一次検定問題 No.02

問題

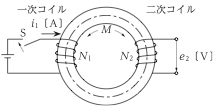
　図に示すスイッチSを投入をしたとき、環状鉄心の一次コイルの電流\( i_1 \) [A] が0.1msの間に0.4A変化し、二次コイルに誘導起電力\( e_2 \) [V] が2V発生した。このときの相互インダクタンスMの値[mH]はいくつか？
　ただし、漏れ磁束はないものとする。

\( e_2 \) [V]は、\( \displaystyle \frac{\Delta i} {\Delta t} \)に比例するので、比例定数をMとすると、

相互誘導起電力は、\( \displaystyle e_2 = -M \frac{\Delta i} {\Delta t} …(1)\)

よって、相互インダクタンスMは、
\( \displaystyle -M = e_2 \frac{\Delta t} {\Delta i} \)

\( \displaystyle \Delta i=0.4, \Delta t=0.1*10^{-3}, e_2=-2 \)

\( \displaystyle M = 2* \frac{0.1*10_{-3}} {0.4} = 0.5*10^{-3}=0.5\)[mH]

参考

電流と磁束からも相互起電力は求められる。
一次コイルの電流が\({\Delta t} \)秒間に\({\Delta I} \)[A]変化して、磁束\({\Delta \phi} \)[Wb]だけ変化した時の二次側の誘導起電力\( e_2 \) [V]は、二次コイルの巻数を\( N_2 \) とすると、相互誘導起電力は
\( \displaystyle e_2 = -N_2 \frac{\Delta \phi} {\Delta t} …(2)\)

(1)と(2)の式の関係から、
\( \displaystyle N_2 \frac{\Delta \phi} {\Delta t} = M \frac{\Delta i} {\Delta t} \)

\( \displaystyle N_2 \Delta \phi = M \Delta i \)より、

相互インダクタンスは、下記の式で求められる。
\( \displaystyle M = N_2 \frac{\Delta \phi}{ \Delta I} \)